Estatística para PMs - Parte 4

Nas três primeiras partes desta série, nós aprendemos a olhar para o passado. Calculamos a média do nosso app de delivery, entendemos a variância das entregas e desenhamos Boxplots para ver onde os usuários se encaixavam. Nós descrevemos a realidade de uma amostra.

Mas a vida de um Product Manager não é feita apenas de descrever o que já aconteceu. Nós somos pagos para tomar decisões sobre o futuro.

• "Se liberarmos essa feature para 1 milhão de usuários, ela vai se comportar do mesmo jeito que se comportou no teste com 1.000 pessoas?"
• "O tempo de entrega caiu de 30 para 29 minutos. Isso é uma melhoria real ou foi pura sorte?"

Aqui termina a Estatística Descritiva e começa a Estatística Inferencial. Hoje vamos entender a matemática que nos permite provar uma sopa inteira provando apenas uma colherada: o Teorema do Limite Central e os Intervalos de Confiança.

O problema da sopa (População vs. Amostra)

Imagine que você está cozinhando um caldeirão gigante de sopa para um batalhão. Você precisa saber se o sal está bom.

Você não bebe o caldeirão inteiro (isso seria inviável). Você mistura bem, pega uma única colher e prova.

Se aquela colher estiver no ponto, você infere que o caldeirão todo está no ponto.

No nosso App de Delivery, é a mesma coisa:

• População (o caldeirão): todos os milhões de pedidos que já aconteceram e vão acontecer. É impossível analisar tudo em tempo real.
• Amostra (a colher): os 500 pedidos que analisamos no teste da semana passada.

A Estatística Inferencial é a garantia matemática de que a sua "colherada" não pegou, por acaso, o único pedaço de batata que estava sem sal.

A mágica matemática: Teorema do Limite Central (TLC)

Este é o conceito mais importante para validar qualquer teste A/B.

Lembra da Parte 3? Vimos que os dados de entrega não seguem uma curva normal bonita. Eles são caóticos: a maioria entrega em 30 min, mas tem uma cauda longa de gente que demora 2 horas.

Se os dados são caóticos, como podemos usar estatística para prever algo? É aqui que o TLC entra.

O teorema: se você tirar várias amostras aleatórias da sua base (ex: pegar a média de entrega de 50 motoboys diferentes todo dia) e colocar essas médias num gráfico, essas médias formarão uma distribuição normal (curva em sino), mesmo que os dados originais sejam uma bagunça.

Exemplo prático no delivery

Imagine que os tempos individuais de entrega são uma loucura ([10, 15, 90, 12, 120...]).

Se você pegar amostras de 100 pedidos e calcular a média delas repetidamente:

• Amostra A: média 28 min.
• Amostra B: média 31 min.
• Amostra C: média 29 min.

Ao plotar essas médias, elas magicamente se organizam em um sino perfeito.

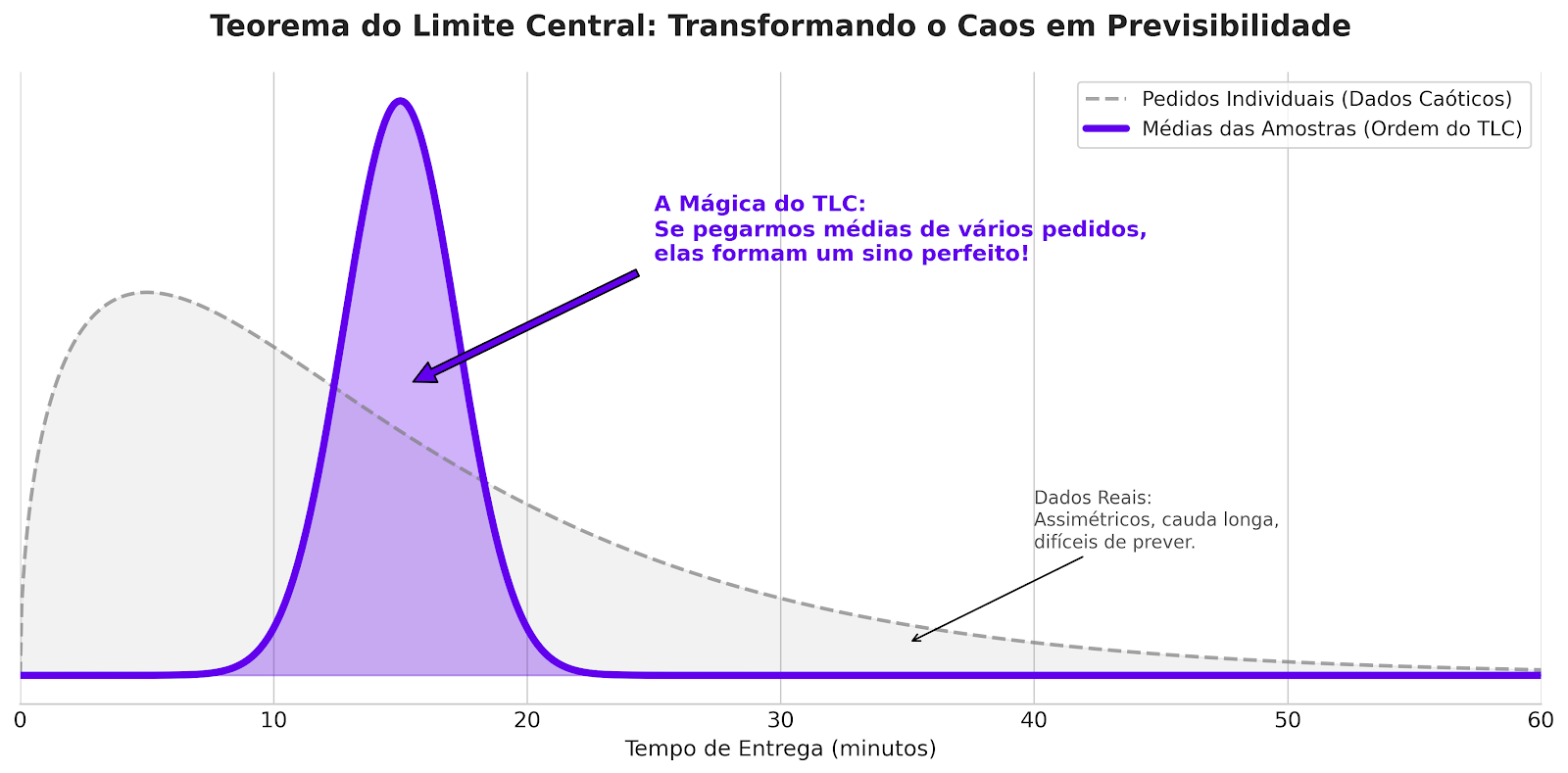
(A linha cinza pontilhada são os dados reais dos pedidos individualmente: caóticos. A linha roxa sólida são as médias das amostras: organizadas e previsíveis.)

Por que isso é importante para o dia a dia do PM?

Graças ao TLC, nós podemos usar a matemática padrão para calcular riscos em testes A/B. Sem ele, não poderíamos confiar que a média de um teste com 1.000 usuários representa a realidade.

Erro Padrão: a precisão da sua colherada

Na Parte 2, calculamos o Desvio Padrão dos nossos pedidos e descobrimos que era de 2,1 minutos. Isso media o quanto um pedido individual variava.

Agora, precisamos do

Erro Padrão (SE). Ele mede a precisão da média do seu teste.

A fórmula é:

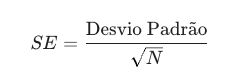
Vamos aplicar números reais do nosso app:

• Cenário A (Discovery Rápido): Você analisou apenas 25 pedidos.

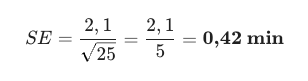
A sua média tem uma margem de erro grande.

• Cenário B (Teste A/B Robusto): Você analisou 1.600 pedidos.

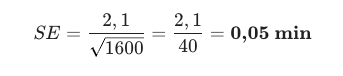
O erro é minúsculo. Sua precisão é cirúrgica.

Algo muito muito importante: Quanto maior o seu N (tamanho da amostra), menor o seu erro. É por isso que não confiamos em testes A/B que rodaram apenas por 2 horas.

Intervalo de Confiança: o fim das certezas absolutas

Números exatos em estatística ("A média é 30") quase sempre estão "errados" porque ignoram o erro padrão que calculamos acima.

O jeito certo de pensar é usando Intervalos de confiança.

Geralmente usamos o intervalo de 95%, que é, grosseiramente falando: Média ± 2x Erro Padrão.

Aplicando ao nosso App de Delivery:

Você rodou um experimento para otimizar rotas.

• Média da Amostra: 29 minutos.
• Erro Padrão (calculado acima): 0,5 minutos.

Seu Intervalo de Confiança é: 29 ± (2 X 0,5). Ou seja: [28 a 30 minutos].

Você diz para o stakeholder: "Com 95% de confiança, o tempo real de entrega está entre 28 e 30 minutos."

A regra de ouro da sobreposição (teste A/B na prática)

Isso resolve 90% das discussões sobre resultados de experimentos.

Imagine que você está comparando a versão atual do app com uma nova versão:

• Versão A (atual): média 30 min. Intervalo: [29 a 31 min].
• Versão B (nova): média 29 min. Intervalo: [28 a 30 min].

O PM afoito diria: "A versão B é 1 minuto mais rápida! Sucesso! Vamos lançar!".

O PM que sabe estatística plota os intervalos e vê isto:

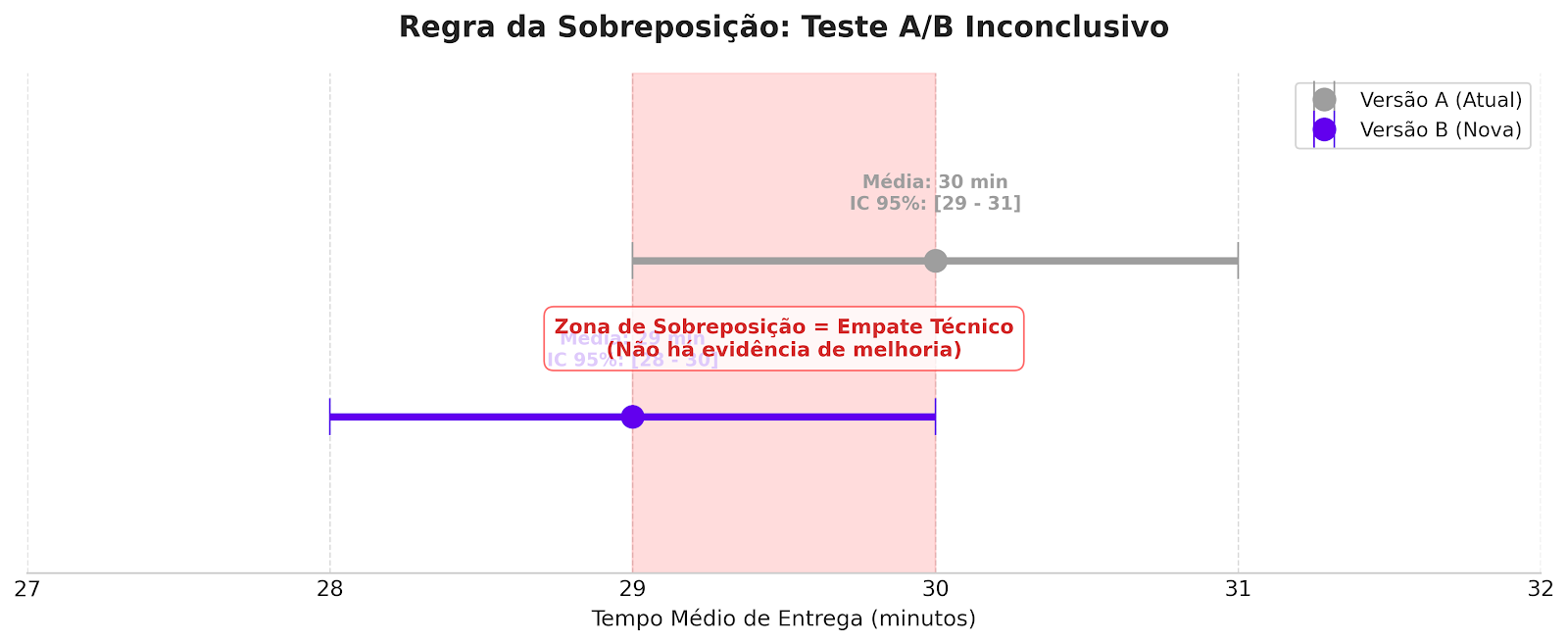
(A zona vermelha é onde os intervalos se cruzam. Se existe cruzamento, existe a chance real de que as duas versões sejam iguais.)

O gráfico mostra que os intervalos se sobrepõem (o intervalo de 29 a 30 minutos existe nas duas versões).

Isso é um empate técnico. Estatisticamente, você não pode afirmar que a versão B é melhor. A diferença pode ter sido mero acaso.

Se você lançasse essa funcionalidade achando que ganhou 1 minuto, estaria apenas adicionando complexidade ao código sem ganho real para o usuário.

Agora você já sabe descrever seus dados e sabe calcular a margem de erro deles. Mas resta a pergunta final, o "santo graal" das decisões de produto:

"Ok, os intervalos não se cruzam e eu tenho um vencedor. Mas como eu provo que foi a minha funcionalidade que causou a melhoria e não o clima, o marketing ou o acaso? Existe relação de causa e efeito?"

Na próxima (e última) parte falarei sobre: teste de Hipótese, valor-P e a diferença real entre correlação e causalidade.

Até lá.